Make a realistic bullets in Unity with C#

Targeting

When you are finished with this section of the tutorial you will have something that looks like this:

Realistic bullets tutorial part 2 finished gif

Part 1. Fire bullets

This tutorial is all about ballistics so I believe the first thing we have to do is to make the turret fire bullets. So create a script called TutorialFireBullets and add the following to it. It's relatively self-explanatory, but the basic idea is to fire a bullet every 2 seconds from the Barrel connector Game Object, so add the script to it.

You also need to add a RigidBody to the bullet so it can fly. Make sure to not add any drag and the mass is not important. The script will give the bullet a speed in the direction the barrel is pointing after parenting the bullet to its parent GameObject so we get a clean workpace. So don't forget to drag the bullet prefab and the Bullets parent Game Object to the script. If you press play you should see bullets fly out of the turret (if you replace TutorialBallistics.bulletSpeed with something like 30f). 

using UnityEngine;
using System.Collections;

public class TutorialFireBullets : MonoBehaviour 
{
    public GameObject bulletObj;
    public Transform bulletParent;
	
    void Start() 
    {
        StartCoroutine(FireBullet());
    }

    public IEnumerator FireBullet() 
    {        
        while (true)
        {
            //Create a new bullet
            GameObject newBullet = Instantiate(bulletObj, transform.position, transform.rotation) as GameObject;

            //Parent it to get a less messy workspace
            newBullet.transform.parent = bulletParent;

            //Add velocity to the bullet with a rigidbody
            newBullet.GetComponent<Rigidbody>().velocity = TutorialBallistics.bulletSpeed * transform.forward;

            yield return new WaitForSeconds(2f);
        }
    }
}

Part 2. Find the angle to hit a target

But bullets flying out from a turret will not kill any targets. What we need is a script called TutorialBallistics, so create it. Also drag the Target cube and the Barrel connector Game Object to the script. Don't worry if you don't understand step size, I can guarantee that you will when the tutorial is over. 

public class TutorialBallistics : MonoBehaviour 
{
    //Drags
    public Transform targetObj;
    public Transform gunObj;

    //The bullet's initial speed in m/s
    //Sniper rifle
    //public static float bulletSpeed = 850f;
    //Test
    public static float bulletSpeed = 20f;

    //The step size
    static float h;

    //For debugging
    private LineRenderer lineRenderer;

    void Awake()
    {
        //Can use a less precise h to speed up calculations
        //Or a more precise to get a more accurate result
        //But lower is not always better because of rounding errors
        h = Time.fixedDeltaTime * 1f;
        
        lineRenderer = GetComponent<LineRenderer>();
    }

    void Update()
    {
        RotateGun();

        //DrawTrajectoryPath();
    }
}

Now we will rotate the barrel so it aims at the target box. To help us we are going to use an equation called Angle theta required to hit coordinate (x,y) from Wikipedia's Trajectory of a projectile. That equation will give us 2 angles or none angles if the target is out of range. The angle in the script called highAngle will rotate the barrel to a rotation similar to an artilley gun, while the lowAngle will give us a rotation similar to a sniper rifle. The artillery will try to hit the target from above, while the sniper rifle will try to hit the target from the front. So create a method called RotateGun. 

//Rotate the gun and the turret
void RotateGun()
{
	//Get the 2 angles
	float? highAngle = 0f;
	float? lowAngle = 0f;
	
	CalculateAngleToHitTarget(out highAngle, out lowAngle);

	//Artillery
	float angle = (float)highAngle;
	//Regular gun
	//float angle = (float)lowAngle;

	//If we are within range
	if (angle != null)
	{
		//Rotate the gun
		//The equation we use assumes that if we are rotating the gun up from the
		//pointing "forward" position, the angle increase from 0, but our gun's angles
		//decreases from 360 degress when we are rotating up
		gunObj.localEulerAngles = new Vector3(360f - angle, 0f, 0f);

		//Rotate the turret towards the target
		transform.LookAt(targetObj);
		transform.eulerAngles = new Vector3(0f, transform.rotation.eulerAngles.y, 0f);
	}
}

...and a method called CalculateAngleToHitTarget() which will apply the equation from Wikipedia. If you then press play you should be able to drag the Target cube around the scene (if you are in Scene view) and the barrel should rotate up and down. 

//Which angle do we need to hit the target?
//Returns 0, 1, or 2 angles depending on if we are within range
void CalculateAngleToHitTarget(out float? theta1, out float? theta2)
{
	//Initial speed
	float v = bulletSpeed;

	Vector3 targetVec = targetObj.position - gunObj.position;

	//Vertical distance
	float y = targetVec.y;

	//Reset y so we can get the horizontal distance x
	targetVec.y = 0f;

	//Horizontal distance
	float x = targetVec.magnitude;

	//Gravity
	float g = 9.81f;


	//Calculate the angles
	
	float vSqr = v * v;

	float underTheRoot = (vSqr * vSqr) - g * (g * x * x + 2 * y * vSqr);

	//Check if we are within range
	if (underTheRoot >= 0f)
	{
		float rightSide = Mathf.Sqrt(underTheRoot);

		float top1 = vSqr + rightSide;
		float top2 = vSqr - rightSide;

		float bottom = g * x;

		theta1 = Mathf.Atan2(top1, bottom) * Mathf.Rad2Deg;
		theta2 = Mathf.Atan2(top2, bottom) * Mathf.Rad2Deg;
	}
	else
	{
		theta1 = null;
		theta2 = null;
	}
}

Part 3. Display the trajectory curve

But wouldn't it be cool to also see the trajectory the bullet takes when it is flying towards the target. If we can make such a trajectory it will also be easier to see what's happening, because bullets are sometimes very fast. So create a method called DrawTrajectoryPath() and add the following. 

//Display the trajectory path with a line renderer
void DrawTrajectoryPath()
{
	//How long did it take to hit the target?
	float timeToHitTarget = CalculateTimeToHitTarget();

	//How many segments we will have
	int maxIndex = Mathf.RoundToInt(timeToHitTarget / h);

	lineRenderer.SetVertexCount(maxIndex);

	//Start values
	Vector3 currentVelocity = gunObj.transform.forward * bulletSpeed;
	Vector3 currentPosition = gunObj.transform.position;

	Vector3 newPosition = Vector3.zero;
	Vector3 newVelocity = Vector3.zero;

	//Build the trajectory line
	for (int index = 0; index < maxIndex; index++)
	{
		lineRenderer.SetPosition(index, currentPosition);

		//Calculate the new position of the bullet
		TutorialBallistics.CurrentIntegrationMethod(h, currentPosition, currentVelocity, out newPosition, out newVelocity);

		currentPosition = newPosition;
		currentVelocity = newVelocity;
	}
}

To make it more good looking I've decided to first calculate the time it takes to hit the target so the trajectory curve stops when the target has been reached. To be able to do that we have to use a method called numerical integration. The basic idea behind that method is to use tiny steps to make our way from the initial position where the bullet starts and move our way to the position where it will land, without firing any bullet in Unity's physics engine. We are simulating the bullet's path.

There are several methods to simulate a bullet's path, but we are here going to begin with a method called Backward Euler, which is similar to the method Unity's physics engine is usings. I tried to find exactly which method the physics engine is using but didn't find any good answer. But Backward Euler will yield a similar path as the path the bullet is flying when it has a RigidBody.

The basic idea behind Forward Euler is that if we know the velocity and position at time zero, we will be able to find the velocity and position in the future. To calculate the velocity we are going to use the small time step h (calculated in the beginning of this section) in this way: velocity_next_update = current_velocity + h * acceleration. And if we know the velocity the bullet has, we can calculate its position in this way: position_next_update = current_position + h * velocity_next_update. And then we repeat the process until we believe we have hit the target while keeping track of the time. So add the mehod CalculateTimeToHitTarget(). 

//How long did it take to reach the target (splash in artillery terms)?
public float CalculateTimeToHitTarget()
{
	//Init values
	Vector3 currentVelocity = gunObj.transform.forward * bulletSpeed;
	Vector3 currentPosition = gunObj.transform.position;

	Vector3 newPosition = Vector3.zero;
	Vector3 newVelocity = Vector3.zero;

	//The total time it will take before we hit the target
	float time = 0f;

	//Limit to 30 seconds to avoid infinite loop if we never reach the target
	for (time = 0f; time < 30f; time += h)
	{
		TutorialBallistics.CurrentIntegrationMethod(h, currentPosition, currentVelocity, out newPosition, out newVelocity);

		//If we are moving downwards and are below the target, then we have hit
		if (newPosition.y < currentPosition.y && newPosition.y < targetObj.position.y)
		{
			//Add 2 times to make sure we end up below the target when we display the path
			time += h * 2f;

			break;
		}

		currentPosition = newPosition;
		currentVelocity = newVelocity;
	}

	return time;
}

...and the method CurrentIntegrationMethod() 

//Easier to change integration method once in this method
public static void CurrentIntegrationMethod(
	float h,
	Vector3 currentPosition,
	Vector3 currentVelocity,
	out Vector3 newPosition,
	out Vector3 newVelocity)
{
	//IntegrationMethods.EulerForward(h, currentPosition, currentVelocity, out newPosition, out newVelocity);
	//IntegrationMethods.Heuns(h, currentPosition, currentVelocity, out newPosition, out newVelocity);
	//IntegrationMethods.RungeKutta(h, currentPosition, currentVelocity, out newPosition, out newVelocity);
	IntegrationMethods.BackwardEuler(h, currentPosition, currentVelocity, out newPosition, out newVelocity);
}

We are here going to experiment with several integration methods, so create a new script called IntegrationMethods where we can store all of them. The first one is Backward Euler. 

using UnityEngine;
using System.Collections;

public class IntegrationMethods : MonoBehaviour 
{
	public static void BackwardEuler(
		float h,
		Vector3 currentPosition,
		Vector3 currentVelocity,
		out Vector3 newPosition,
		out Vector3 newVelocity)
	{
		//Init acceleration
		//Gravity
		Vector3 acceleartionFactor = Physics.gravity;

		//Main algorithm
		newVelocity = currentVelocity + h * acceleartionFactor;

		newPosition = currentPosition + h * newVelocity;
	}
}

If you now press play you should see a nice trajectory line from the turret towards the target. And the bullets fired from the turret should follow that path.


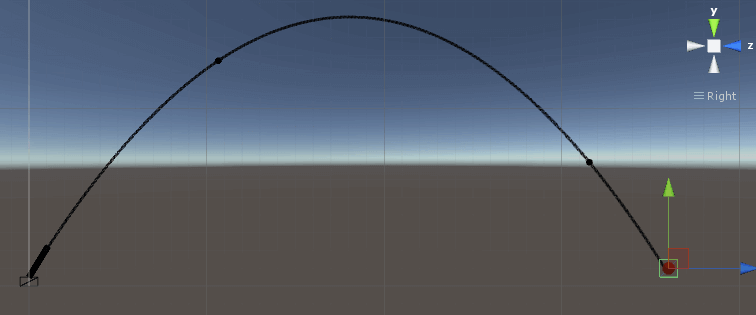
How the trajectory path looks like with Backward Euler

But if you move the target as little as 40 meters away from the turret, you will se that the trajectory line is not crossing the center of the target, and neither are the bullets. They are still hitting the box, but as we move the box further away from the turret, the accuracy will continue to fall. And that is not good enough if we want realistic bullets.

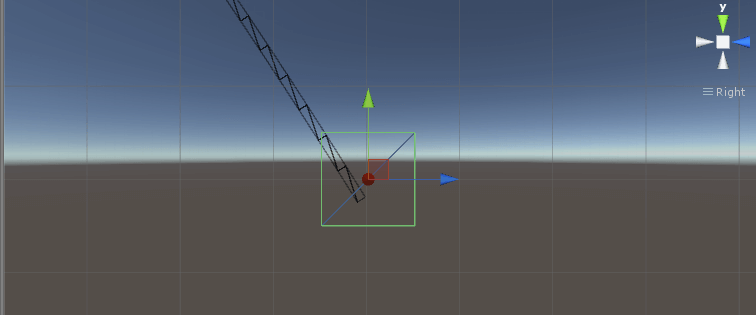
Bullet accuracy with Backward Euler

You can change the time step value h to a smaller value, which will improve the accuracy of the line, but the accuracy will not be nearly 100 percent as good as we want it. Also, if you decrease the time step h to a too small value, you will get rounding erros that will decrease the accuracy as if you had a large h. So h can't be neither too small nor too large. h has to be "lagom" as we say in Sweden. And how do we increase the accuracy of the bullets? That is the topic of the next part.


Back